548. Планирование полета
Авиакомпания
"NCPC Авиалинии" выполняет полеты между n городами, пронумерованными от 1 до n, по всему миру. Однако у нее имеется только n – 1 различных рейсов (в обоих направлениях), поэтому для
путешествия между любыми двумя городами приходится пользоваться несколькими
рейсами. Поскольку менеджмент убедился, что существует возможность
путешествовать между любыми двумя городами, то существует в точности одно
множество рейсов, которыми может воспользоваться пассажир для перемещения между
двумя городами (считая что Вы воспользуетесь только одной авиалинией).
В последнее
время в NCPC Авиалиниях многие часто летающие пассажиры жаловались, что им приходится слишком часто
менять рейсы, чтобы добраться до конечного пункта назначения. Поскольку NCPC
Авиалинии не хотят потерять своих клиентов, и при этом сохранить удобство своих
рейсов, они решили отменить один из своих рейсов и заменить его другим.
Помогите авиакомпании написать программу, которая поможет найти рейс, который
следует отменить, а также новый рейс, который следует добавить, чтобы
максимальное количество смены рейсов пассажиром при путешествии между парами
городов, которые обслуживают NCPC Авиалинии, было минимальным.
Входные данные
будут таковыми, что всегда можно улучшить максимальное число смены рейсов.
Вход. Первая строка содержит количество
городов n (4 ≤ n ≤ 2500) в авиалиниях NCPC.
Следующие n – 1 строка описывает
рейсы. Каждый рейс задается парой городов a
и b (1 ≤ a, b ≤ n).
Выход. Вывести
следует три строки. Первая строка содержит наименьшее количество рейсов,
которое следует сменить при путешествии между парами городов после изменения
одного из рейсов. Вторая строка содержит номера городов отменяемого рейса.
Третья строка содержит номера городов, между которыми будет добавлен новый
рейс.
Если существует
несколько решений, вывести любое.
|
Пример входа |
Пример выхода |
|
4 1 2 2 3 3 4 |
2 3 4 2 4 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
Поскольку
входной граф представляет собой дерево и n
≤ 2500, то количество ребер не больше 2500. Переберем все ребра,
попробовав удалить соответствующий рейс. После удаления ребра получим два
дерева t1 и t2. Пусть их диаметры
соответственно равны diam1
и diam2. Новый маршрут
должен соединять центры этих деревьев. После его добавления получим дерево с
диаметром
max(diam1, diam2, ![]() +
+ ![]() + 1)
+ 1)
Теорема. Если диаметр
дерева равен d, то максимальное
расстояние от его центра до вершин равно ![]() .
.
Осталось найти
такое ребро, после удаления которого в результате соединения центров полученных
деревьев образуется дерево минимального диаметра.
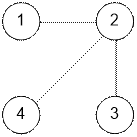
Пример
Слева
представлен входной граф, его диаметр равен 3.
Справа – после
изменения одного рейса, его диаметр равен 2.

Реализация алгоритма
Объявим глобальные константы и массивы.
#define MAX 2510
#define INF 2000000000
vector<vector<int> > g;
int next[MAX];
Запускаем поиск в глубину из
вершины v. Вершина prev хранит предка v. Движение по ребру (v1,
v2) запрещено в обоих
направлениях (оно считается удаленным). В процессе поиска строим массив next:
если из вершины v переходим к to, то положим next[v] = to.
Функция depth возвращает
расстояние от v до самой дальней
вершины дерева.
int depth(int
v, int prev = -1)
{
int height =
0;
next[v] = v;
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if ((v ==
v1) && (to == v2)) continue;
if ((to ==
v1) && (v == v2)) continue;
if (to !=
prev)
{
int h =
depth(to,v) + 1;
if (h
> height)
{
height = h;
next[v] = to;
}
}
}
return
height;
}
Стартуем из вершины v и двигаемся по ребрам дерева поиска в
глубину steps шагов.
int RunTree(int
v, int steps)
{
for (int i = 0; i < steps; i++)
v = next[v];
return v;
}
Основная часть программы. Читаем
входные данные, строим граф.
scanf("%d", &n);
g.resize(n+1);
for(i = 0; i < n - 1; i++)
{
scanf("%d
%d", &u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
memset(next,-1,sizeof(next));
res = INF;
Перебираем ребра графа.
for(i = 1; i <= n; i++)
for(j = 0; j
< g[i].size();j++)
{
int to =
g[i][j];
v1 = i; v2 = to;
Пробуем выбросить ребро (i, to)
= (v1, v2), получив два отдельных дерева.
int d1 =
depth(v1);
int d2 =
depth(v2);
int u1 =
RunTree(v1,d1);
int u2 =
RunTree(v2,d2);
Вычисляем диаметры деревьев.
int diam1
= depth(u1);
int diam2
= depth(u2);
int
CurDiam = max(max(diam1,diam2),(diam1+1)/2 + (diam2+1)/2 + 1);
if
(CurDiam < res)
{
Удаляем ребро (del1, del2) и добавляем (add1,
add2).
res = CurDiam;
del1 = v1; del2 = v2;
add1 = RunTree(u1, diam1/2);
add2 = RunTree(u2, diam2/2);
}
}
Выводим ответ.
printf("%d\n%d
%d\n%d %d\n",res,del1,del2,add1,add2);